Die Welt der Schwingungen
Pendelschwingungen
Im 16. Jahrhundert beobachtete Galileo Galilei im Dom zu Pisa die dort hängenden Lampen und deren Pendelbewegungen. Dies regte ihn zur Entdeckung der Formel zur Berechnung der Pendelfrequenz an.
Wie oft ein Pendel pro Minute hin und her schwingt, ist abhängig von der Pendellänge. Je kürzer das Pendel von der Aufhängung bis zum Schwerpunkt, umso höher ist die Pendelfrequenz. Ein Viertel der Länge schwingt mit doppelter Frequenz.
Ausschlaggebend für die genaue Berechnung ist zudem die Fallbeschleunigung, die auf unserem Planeten 981cm pro Sekunde im Quadrat ist.
Die Pendelformel
Die Formel enthält folgende Angaben:
g = 981 cm . sec-2 = Fallbeschleunigung
l = Länge (von Aufhängung bis Schwerpunkt)
π = 3,14159 (die Kreiszahl)
T = Dauer einer ganzen Pendelperiode
(hin + her)
(T = 1 : Frequenz)
Ist die Pendelperiode bekannt, kann die Länge das Pendels berechnet werden, oder umgekehrt aus einer gegebenen Länge die Periode.
Die Formel zur Berechnung der Dauer lautet:
T = 2 . π . √ (l:g)
Diese aufgelöst zur Berechnung der Länge:
l = T2 . g : (4 . π-2)
oder zweckmäßig umgeformt
l = T2. g . π-2 . 0,25 =
l = T2 . 24,85 cm . sec-2
Um die Pendellänge zu erhalten ist nur die Zeit zu quadrieren und dann mit 24,85 zu multiplizieren.
Das Erdenjahr-Pendel
Als Beispiel die Berechnung der oktavanalog zum Erde-Sonnenumlauf pendelnden Länge:
Die 25. Oktave von 1 x pro Jahr ist
63,8 bpm (beats per minute), bzw. 1,0633 Hz (per sec).
T = 1 : 1,0633 Hz = 0,94047 sec
0,940472 . 24,85 = 22 cm
In der Tabelle der Stimmdaten auf Seite 19 sind die Oktavtempi des Sonnensystems und die jeweiligen Pendellängen aufgeführt. Für ein doppelt so schnelles Tempo gilt ein Viertel der Pendellänge bzw. für das halbe Tempo die vierfache Länge.
Die Grafiken auf der folgenden Seite und auf der Rückseite dieser Broschüre kann nur in der Druckausgabe als originales Pendelmaß der planetaren Zyklen verwendet werden. Ein Maßband zum Ausdrucken findet sich unter planetware.de/download/Pendelmassband.pdf
Pendelmaße astronomischer Zyklen
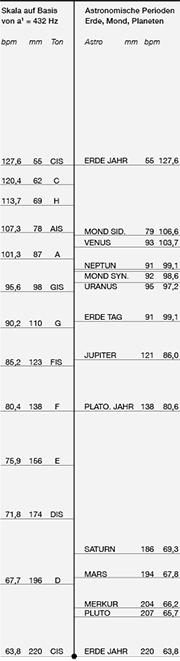
In der nebenstehenden Tabelle sind rechts der senkrechten Linie die Pendellängen für die oktav-analogen Tempi der Zyklen von Erde, Mond und Planeten angegeben. Links stehen die Daten einer chromatischen Tonleiter von Cis bis Cis, basierend auf dem Kammerton a1 = 432 Hz.
Das Cis des Erdenjahres (136,10 Hz) entspricht dieser Kammertonhöhe. Sechs Oktaven tiefer ergibt sich daraus ein musikalisches Tempo von 127,6 Schlägen pro Minute. Ein 5,5 cm langes Pendel schwingt genau in diesem Tempo. Ein Pendel von vierfacher Länge (22 cm) bewegt sich eine Oktave tiefer mit 63,8 Schlägen pro Minute.
Die Tabelle rechts und die Abbildung auf der Rückseite können als Maßband dienen, um die Länge eines Pendelfadens einzustellen und das Pendel wie ein Metronom als Taktgeber zu nutzen. Von der Aufhängung bis zum Schwerpunkt sind es, wie angegeben, 220 mm. Bei einem kugelförmigen Gewicht liegt der Schwerpunkt in der Mitte der Kugel.
Ein Pendel verdeutlicht anschaulich das Gesetz der Kosmischen Oktave: Das 22 cm lange Pendel benötigt 0,94047 Sekunden für eine Hin- und Herbewegung. Verdoppelt man diese Zeit 25-mal, ergibt sich exakt die Dauer eines Jahres – der Umlaufzeit der Erde um die Sonne. Die Formel zur Berechnung der Pendellänge für eine bestimmte Frequenz oder Schwingungsdauer steht auf der vorherigen Seite.
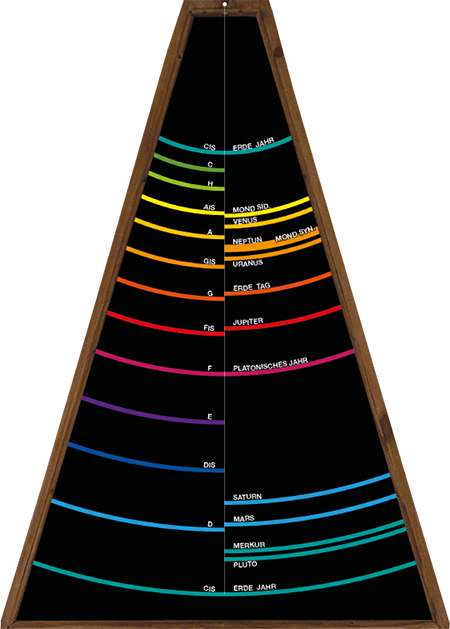
Nachdem Hans Cousto im Oktober 1978 aus den astronomischen Perioden des Sonnensystems deren Oktavtempi, -töne und -farben berechnet hatte, baute sein Mitbewohner Rainer Kohlwald den hier abgebildeten Pendel-Leuchtkasten. Die Farben entsprechen den Pendelfrequenzen in oktav-analoger Zuordnung. Die Abbildung auf der Rückseite dieser Broschüre zeigt eine grafische Rekonstruktion im Maßstab 1:4 des Originals: der Holzrahmen basiert auf einem Foto, die schwarze Front mit den Farbfolien wurde nachkonstruiert.
Von Fritz Dobretzberger lizensiert unter CC BY-NC-SA 4.0
Nichtkommerzielle Weitergabe unter gleichen Bedingungen